New Year Count-up - When math and chess entwine
"A chess problem is an exercise in Pure Mathematics", Godfrey Harold Hardy had famously opined in his book "A Mathematician's Apology". Chess has been compared to mathematics time and time again, and figuratively it makes sense for the game no doubt embodies many elements which are distinctly mathematical in nature. But what if these two very different pursuits of human intellect are brought literally together under one umbrella? What would a juxtaposition of chess and math actually look like? In today's article the authors Satanick Mukhuty and Andrew Buchanan probe deeply into this question!
Chess, Math, Retros - A different way to celebrate New Year!
By Satanick Mukhuty
Last year I came across a curious chess-math challenge that was posed by my friend Andrew Buchanan on his Facebook timeline. The following was the position he shared and the task was neither to checkmate nor to win but to find the number of legal sequences that led to it!
Andrew Buchanan, Facebook 1st January 2019

I knew that this was a problem in what is known as Retrograde Analysis which Andrew specializes in. In a Retrograde problem (or retro, as it is more commonly called) the solver's main challenge lies in reverse engineering the position he is given. As opposed to more orthodox compositions involving the calculation of forward variations leading to checkmate or win, a retro is all about thinking backwards. In this case, for instance, a thorough detective investigation of how the position arose after 11 moves by Black and 12 by White strikingly reveals the most singular of nuances.
Observe, the distribution of white pieces shows exactly 10 displacements which account for at least 10 moves. Now since White played only 12 moves in total, it is natural that some of the four missing white pieces never made a move and were actually captured on their initial home squares. But what black piece could have come all the way to the first rank and returned back in just 11 moves? A little introspection makes it apparent that it wasn't a piece but the missing pawn on g7 that made all the way into White's camp, captured on the first rank and promoted. Here's a sample sequence of how things went: 1.d4 Nh6 2.Bxh6 e5 3.e3 exd4 4.Bb5 dxe3 5.c4 g5 6.Nc3 g4 7.Qe2 g3 8.O-O-O (obviously castling is the optimal way to get the wK to c2 and a1 rook to f3) 8...gxh2 9.f4 hxg1=N 10.Rf1 Nh3 11.Rf3 Nf2 12.Rhh3
The above Proof Game shows the shortest way to reach the given position but it is far from unique and has many (too many!) transpositions. This brings us to the second part of the problem, the mathematical part. How to go about counting all these transpositions? Well, let's summon some highschool combinatorial skills and analyse!
Firstly, we observe that the head and the tail of the sequence, that is the starting 1.5 moves 1.d4 Nh6 2.Bxh6 and the ending 1.5 moves 11.Rf3 Nf2 12.Rhh3, will remain invariant in all sequences no matter what. The transpositions will lie all in the middle. Now, the eight white moves in the middle will be in the following order: e3 > Bb5 > c4 > Nc3 > (Qe2) > 0-0-0 > Rf1 > (f4) except that Qe2 can vary in 3rd, 4th, 5th positions and f4 can vary in all eight positions. So there are 8×3=24 ways in which white's half-moves can occur in the middle. Next, we are to count the 9 black moves. This will be in two parts consisting of the ordered 3 and 6-tuples, e5 > exd4 > dxe3 and g5 > g4 > g3 > gxh2 > hxg1=N > Nh1. These two parts can be combined in 9 choose 6 (9 choose 3) = 84 ways. So the total number of transpositions (independent white and black moves combined) we are arriving at is 84×24=2016. But is 2016 the answer? Remember this problem was posted on the 1st of January 2019 and therefore was meant to have exactly 2019 solutions (New Year after all!). So we are almost there but somehow short of three solutions!
I remember to have arrived at 2016 fairly easily (albeit making a silly arithmetic mistake!) but the missing three solutions eluded me for a whole afternoon. I also remember the joy I felt when after hours of brooding it suddenly occurred to me that the above Proof Games had two of the special three moves - castling and promotion - so the final piece of the puzzle might as well involve the third special move, namely en passant! That was it, I realized that the solution was staring me right in the face! The missing three were simply the sequences starting with 1.d4 Nh6 2.Bxh6 e5 3.f4 exd4 4.exd3 en passant. There could be only three trivial transpositions possible with this using Q, N, and wPc2. Therefore the final answer was 2016+3 = 2019. How incredible! Three themes: castling, promotion, and en passant, in a single problem. The Valladao Task!
This year Andrew has composed two more New Year problems and has sent both of them to ChessBase India as originals. But before we present them to you here is a brief but ingenious elucidation by Andrew himself on how in general one goes about solving and also composing such problems!
A Short History of New Year’s Proof Games
By Andrew Buchanan
Every year since 2004, Noam Elkies has published a New Year's proof game, where the number of solutions exactly equals the number of the coming year in the Western Calendar. These kinds of problem, which can extend beyond proof games to other genres, can be broadly termed as "path enumeration" and they work by embedding certain simple combinatorial identity into a chess game. By 2015, I had seen how much fun Noam was having, so I decided to join in, and have been humbly submitting alternative compositions since that year. In order to explain these problems, I’ve put together some terminology, around a garment metaphor. I hope it enlightens and also entertains you!

The raw material to fabricate specific numbers in these problems are almost always threads. A thread of length m, denoted by m_, is a sequence of m moves which must be played in that order by a single player, but not necessarily consecutively. But m_ can only generate one solution path, whatever the value of m. Now to get multiple paths, we weave threads together. This is like riffling two stacks of playing cards together. So for example the five White moves a4, a5, a6, h4 and h5 form two threads a4 > a5 > a6; and h4 > h5. The a-pawn and h-pawn move independently of one another, so there are “5-choose-2” (denoted C(5,2)) = (5!/3!2!) = 10 different orders possible for these 5 moves. So any small number in Pascal’s triangle is easy to fabricate.
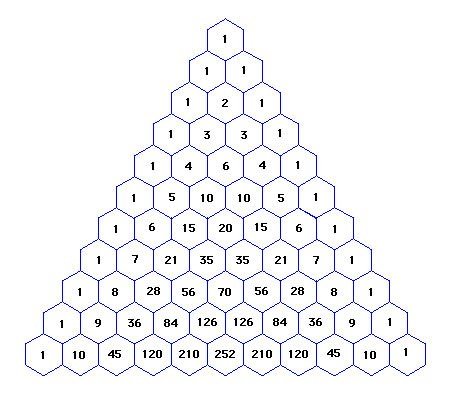
But a simple weave rarely hits the target total directly, and honestly would be a bit boring if it did. We want to assemble more complicated fabrics, and have other ways to combine pieces of fabric together to make larger ones. A common trick is to stitch one fabric to another, where every move in the first fabric must precede every move in the second. We can stitch two threads together, and then just get a longer thread. If we put a thread on the end of a weave, then we call this a hem. For example, consider the three white moves a4, b3, and Ba3. a4 and b3 can be woven together in C(2,1) = 2 ways, and then after the weave we have the 1-thread Ba3. A hem is a neat way to tidy up a piece of fabric, and so is an aesthetic feature. Other more general stitches are also possible.
Another mechanism you will see is the split. Here, one of the pieces has multiple routes to reach its destination. And you need to consider all in turn - then these contributions can be added together. A third common trick is the cut-out. Here two sets of possibilities are mostly independent, so the paths can nearly be multiplied together. But there is some special case where the pieces interfere with one another, and this needs to be subtracted from the product. For example Nc3 > Na4 and c4 > Qc2 is not a weave because N on c3 will block c4. This could only happen if (impossibly) Nc3 > c4. So this is cut-out.
Now let's tackle a problem and see some concrete application of the "theory" above.
Noam Elkies, The Electronic Journal of Combinatorics 2004

The first problem is a Series Proof Game, which means that White makes 12 moves in a row here, with no black moves at all, so for simplicity we don’t show any black units. As far as I remember this was the very first New Year problem composed by Noam.
The diagram shows three threads:
i) Nf3 > Ne5 > f3 > Kf2 > Ke3 > Kd? > Kc? > Kb5
ii) c4 > Nc3 > Rb1
iii) g3
But look: in (i) wK has three possible routes from e3 to b5: -Kd3-c4; -Kd4-c4; -Kd4-c5
If wK goes via c5, it never engages with the wcP. The two threads are independent and weave together, so we have C(11,3) paths. On the other hand, if wK goes via c4, it must leave for b5 before c4 ever happens. In that case, the two threads are stitched as (i) must come before (ii). Stitching two threads gives us one longer thread. So this contributes 2 paths to the total. C(11,3)+2 = 167 paths.
However, we also have (iii) which weaves with the piece of fabric we have just made. The one move can weave into the 11 moves of the other piece of fabric in 12 ways: we can write this as C(12,1)=12. 12×167=2004 paths.
François Labelle, Retro Mailing list 2004

The above also has 2004 solutions but this in contrast was discovered and verified by a computer. For such short games, a skillful programmer using a powerful computer can “strip mine” all the positions achievable in a small number of moves, and identify those that can be achieved in any given number of ways. François Labelle is a world leader in this kind of work. But the combinational logic is fragmented into a myriad shards here, and there is no fun-to-find combinatorial identity. I include it here by way of contrast with Noam's problem, which reminds me of an electronic solar panel compared to François's as a chlorophyll-rich leaf. The energy cycle in photosynthesis is not entirely understood, and is very efficient, after taking millions of years to evolve. A solar panel is understandable, and much less efficient, but can be fabricated by humans!
Sometimes, Noam and I have tried to follow a principle proposed by Richard Stanley: all solutions to a problem should involve exactly the same moves, just in different orders. This is related to the idea of taking a partial order and determining how many total orders (“linear extensions”) are consistent with it. However, my feeling is that spatial relationships are more complicated and can be more fun. Nevertheless, this was a worthy goal that we attempted.
The Stanley principle is subtractive: one starts with a potentially larger number of possible sequences, and some sequences are removed, because they don't work. The years running up to 2016 were particularly easy to apply this approach, as 2016 has many small factors. However, from 2017 onwards we entered a phase when Stanley's principle is harder to apply. So we have become more flexible now.
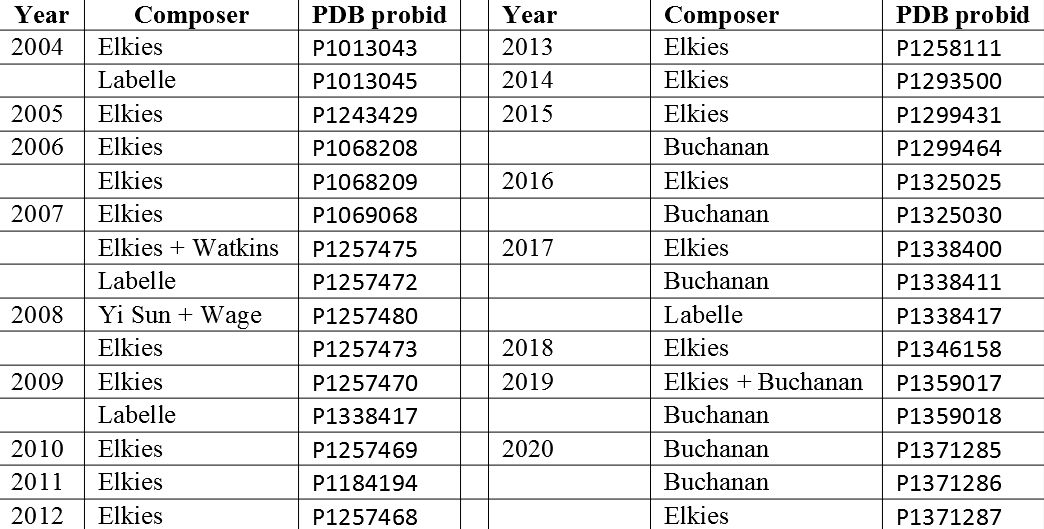
The following table lists the main New Year’s compositions, focusing on the Western calendar problems composed before that year had elapsed, rather than retrospectively. To have a go at these visit the Chess Problem Database and use the search option. For example if you want to access the 2019 problem by Elkies and Buchanan then just type PROBID='P1359017' in the search box and click 'search'.
Two New Compositions
By Andrew Buchanan
Let’s bring it bang up to date and usher in the New Year with two new problems. There are two this time to give me insurance against a repeat of a collision with Noam that happened in 2019!
Andrew Buchanan, Original 2020

Before d3, the two threads a4 > Ra3 > Rf3 and e4 > Bc4 must happen. There are C(5,2) = 5!/3!2! = 10 possible orders in which these two threads can be woven together, and the choice is entirely independent of the rest of the moves. So without loss of generality pick: a4 > Ra3 > Rf3 > e4 > Bc4 > d3 and remember we have a factor of 10 for the overall path enumeration.
This thread continues... d3 > Bf4 > Nd2 > Qa1 > Qa3, giving length 10, and there is another length 3 thread h4 > Rh3 > Bh2. The only connection between these threads is that Bf4 > Bh2. This seems a bit fiddly to count directly. Is there an easy way?
Suppose we lived in a crazy world where these two moves by wQB could occur in either order. Then the 10-thread and the 3-thread would be independent, and they could be stitched together in C(13,3) = 13!/10!3! = 286 orders. On the other hand, suppose we lived in a different crazy world where the second move by wQB must take place before the first one. Then the final moves must be Bf4 > Nd2 > Qa1 > Qa3. Then the preceding moves form a 6-thread and the 3-thread. C(9,3) = 9!/6!3! = 84 orders.
The point is that the difference between the two crazy values is exactly the number of orders with the two wQB moves in the correct order: 286-84=202. This is just the application of the cut-out principle discussed above. Multiplying this by the factor of 10 gives us 2020 paths.
Andrew Buchanan, Original 2020

It looks like a Wh pawn promoted on a8. Let’s try a line which turns out not to work. Say that wKB never moved. Then the game could go something like: 1. a4 d5 2. h3 Bxh3 3. a5 Bg4 4. Rh6 Bxe2 5. Rd6 g6 6. a6 e6 7. axb7 Qf6 8. bxa8=N Be7 9. Nb6 Bd8 10. Nc8 Ne7 and Wh is just too late to sac N on e7. There is no way that Wh can execute a Ceriani-Frolkin capture. Note: Ceriani-Frolkin is a popular retro theme that refers to the effect of a promotion followed by the capture of the promotee.
Instead wBf1 looks like it is Pronkin, that is a promoted imposter. The following Wh threads of moves exist:
- a4 > a5 > a6 > a7 > a8=B > Bg2 > Bf1
- c4 > cxd5 > dxe6 > Bg2 > Bf1
Note that both threads end with Bg2 > Bf1. So a 5-thread and a 3-thread are woven, hemmed by a 2-thread. There’s also the possibility of en passant, but let’s put that aside for now.
The game must begin: 1. X d5 2. Y Bxh3 3. Z Bxf1 4. Rh6 Bxe2 5. Rd6, releasing both the Black threads:
- e6 > Qf6 > Be7 > Bd8 > Se7 >> 0-0 > Kh8 > Rg8 > Rg7
- g6 and then > Rg7
So an 8-thread and a 1-thread are woven, hemmed by a 1-thread.
If we return to the first three Wh moves, one must be h3, another must be g3, while the third is the first move of the Wh weave (5_1 or 3_1). There are apparently 6 possible orders for the 3 moves, but it’s clear that h3 cannot be third, due to 2… Bxh3. So there are 4 orders possible for these 3 moves.
The Wh weave can occur in C(5,3) orders = 8!/5!/3! = 56. The fact that the first move of these 8 can transpose with h3 or g3 does not affect the sums beyond the calculated factor of 4. The Bl weave can occur in C(8,1) orders = 9. So we have 56×9×4 = 2016 orders. But what about en passant? In this case, Bl plays e5 instead of e6, but must do it at the right time. It turns out that White must play for the en passant as quickly as possible, while Black must delay as long as possible: 1. X d5 2. Y Bxh3 3. Z Bxf1 4. Rh6 Bxe2 5. Rd6 g6 6. cxd5 e5 7. dxe6 (e.p) etc. But now both Wh and Bl have exhausted one of their threads, so the rest of the game is deterministic. So this gives just another 1×4 = 4 orders. The total is therefore 2020 orders!
Those who are paying attention may have noticed similarities in structure with the 2019 problem that Satanick solved in the first section. Both feature Valladao, and have a base 2016 solutions, with several more provided by en passant. However the 2020 effort extends the promotion to a Pronkin Theme, whereby a promoted unit returns to the a square corresponding to his type. Spot the clean hems on this garment too!
Another new problem by Noam Elkies
By Satanick Mukhuty
We thank Noam Elkies for allowing us to publish his freshly minted New Year problem as an original on our website. Readers are encouraged to give this last problem a serious try before looking at the analysis below!
Noam Elkies, Original 2020

Can you come up with one sample series PG in 24? If you can then the threads to work with should be clear. Very briefly, here we have a long 21-move thread h4 > Rh3 > Ra3 > Ra5 > a4 > Ra3 > Rc3 > b3 > Ba3 > Bd6 > Bh2 > f4 > Kf2 > Ke3 > Kd4 > Kc5 > Kb6 > Rc5 > c4 > Nc3 > Qa1 and a short 3-move thread g4 > Bg2 > Bh1 which are connected by h4 > Rh3 > Bh1. The 21-move thread and 3-move thread can be weaved into each other in C(24,3) = (24!/3!21!) = 2024 ways but from this we have to cut-out all the possibilities where Bh1 happens (impossibly) before Rh3 and this is just the number of ways we can weave h4 and the 3-thread g4 > Bg2 > Bh1 together which is C(3+1,1) = C(4,1) = 4. Thus, the answer is 2024 - 4 = 2020
The number 2020 has been split in three different ways in the last three problems. Ambitious readers might want to take up the challenge of invoking other combinatorial identities to arrive at the same target figure via different routes. Or perhaps some readers may be even consider working towards the next year's New Year problem! If you have any ideas do share it in the comments below. We sign off for now by wishing you a very happy and prosperous 2020.
About the authors

Satanick Mukhuty is an author, editor, and social media manager at ChessBase India. He has a background in Mathematics. He is an avid enthusiast of composition chess and is sincerely committed to promoting it around the world.

Andrew Buchanan is an itinerant IT consultant, currently living and working in Singapore, who has been interested in chess problems, principally retros, since 2001














































